Lab Report of Density of Solids 1
by Ahmed Adil, Faiyaz Habib, Francisco Martinez and Nasif Khan
City College of New York
Author Note
This paper was written for English 21007, Writing for Engineers, taught by Professor Susan Delamare. Correspondence concerning this paper should be addressed to
Contact: [email protected], [email protected], [email protected], [email protected]
Table of Contents
Abstract————————————————————————— p. 3
Introduction———————————————————————- p. 4
Materials————————————————————————– p. 5
Procedure————————————————————————- p. 6
Results and Discussion———————————————————- p. 7
Conclusion———————————————————————— p. 7
Appendix————————————————————————– p. 8
List of Illustrations————————————————————— p. 10
References————————————————————————- p. 11
Abstract
Measuring the density of different samples and sizes are found to be a ratio between the mass and volume. This simple formula, d = m/v, is a crucial understanding for a wide range of experiments, whether it be measuring the lipoproteins in a species of animals, or using it to explore different properties. In this study, we measure the effectiveness of the water displacement method, by measuring the density of six aluminum objects and of an unknown material. We compare their average density with their real density, excluding the unknown material, since the object and consequently its density, is not known. Lastly we analyze the range of the accuracy of the results. In the aluminum experiments the average density of the material was 2.7 g/ml with most results ranging between 2.6 g/ml and 2.9 g/ml with only one result of 2.4 g/ml, which illustrates the precision of the water displacement method. Aluminum has a density of 2.7 which matches our average density. The unknown object cannot be compared to its actual density because the material used is unknown. However, the data was consistently ranging from 5 g/ml to 8.8g/ml with an average density of 8.2 g/ml, which is a good sign that the real density should be at that range near the average. An important note is that many materials that react to water would not be suitable for the water displacement method since these reactions can affect the accuracy of the data. Also the more iterations of measuring an object’s density leads to a closer measurement to the object’s average density. With these considerations, the data of our experiment suggests that the water displacement method is a valid tool for measuring density.
Introduction
The Density of an object is very valuable information that is commonly used in many scientific fields. The density of an object is calculated by dividing the mass of the object over the volume. Therefore the formula of an object’s density is D = m / v. Where d is the density of the object, m is the mass of the object, and v is the volume of the object. Inversely, possessing the density of an object allows the mass to be calculated by multiplying the density with the volume. In addition, the volume can be calculated by dividing the density of the mass.
Figure 1 – Formula for Density, in terms of mass and volume
Reprinted From:
https://ubisafe.org/explore/formulas-clipart-density/
This relationship between density, mass, and volume are universally constrained which makes density versatile in a wide range of experiments in and out of a lab. This property of interchangeability between the values of density, mass, and volume, is what makes the density of an object a powerful tool in many fields of science. For instance, this interchangeability was used to measure the volume of density cups. (Vinkovic, n.d.).
The density measurement itself is valuable information that is used in many modern studies. In an experiment measuring the proteins in the Lycosa tarantula, a burrowing wolf spider, they found that the density body condition (statistically measured with the body’s volume and size) was able to detect greater differences on the binary response variables, compared to classic mass/size or volume/size indices (Lorano, 2008). Meaning that using the density was more accurate at measuring binary response variables, than using the ratios of mass/size or volume/size indices.
Due to the significance of the density of an object, a simple method for determining the density of an object for all shapes, at an inexpensive cost point would facilitate scientific research, and allow for the more frequent use of applying density in experiments. A frequent method used for this is the water displacement method, where weight and water displacement of an object is used to measure density. In fact many modern techniques for measuring density, use the water displacement method as a foundation. Microgram-sized biological samples were measured in a liquid solution where a sensor was used instead of water displacement (Oskui, 2017). However the principle between using the sensors and the water displacement method is very similar. Sensors measure the difference in displacement instead because the microgram-sized biological samples in their native liquid environments cannot be measured visually. In this study, the effectiveness of the water displacement method will be analyzed. The water displacement method has the advantages of being low cost, practical and even more precise than other methods, such as the sand displacement method, with the assumption that the material examined has low reactivity to water (Gupta, T et al, 2016). For this reason we chose to use aluminum and an unnamed material to be measured, with the purpose of testing the water displacement method, graphing the data and comparing it with its known density in order to investigate how accurate of a method it
Materials
The purpose of this experiment is to measure the density as a ratio of the mass of an object to its volume. We will be measuring the volume using the water displacement method with the measuring cylinder, and the mass of an object with a laboratory balance.
- Measuring Cylinder
Figure 2 – Measuring Cylinder
Reprinted From:
http://www.serrata.com.au/products/category/XLPLWHFG-measuring-cylinder
This instrument is useful in measuring accuracy. Cylinders with different measures re graduated differently. When operating this instrument, one must maintain a proper eye level and making sure the cylinder is on a balanced surface. For this experiment, we will be using 25 mL cylinders.
- Laboratory Balance
Figure 3 – Electronic Laboratory Balance
Reprinted From:
For this experiment, we will be using top loading electronic balances.
Procedure
For this experiment, we will be working with 6 aluminum samples and 6 unknown material samples. In order to calculate the density, we will need to identify the mass and volume of each sample. This will take place by weighing to cover the object you are measuring the volume of (~10 mL of water)
- Measure the exact volume of water
- Tilt the cylinder and carefully submerge the sample by sliding it down the side (avoid splashing any water or break the cylinder)
- Read the volume of water with the submerged sample.
- Find the volume of the specimen by calculating the difference in the two volumes. Record the number.
- Repeat steps 1-5 for all 12 samples.
This will allow you to calculate the density for each of your samples by dividing the recorded mass over the volume.
Results and Discussion
There are six samples of the aluminum and the anonymous material that was measured in this experiment. In the aluminum experiments the average density of the material was 2.7 g/ml with most results ranging between 2.6 g/ml and 2.9 g/ml with only one result of 2.4 g/ml which illustrates the precision of the water displacement method. Aluminum has a density of 2.7 which matches our average density. The precision and the accuracy of the data reinforces the validity of using the water displacement method for measuring density. The unknown object cannot be compared to its actual density because the material used is unknown. However, the data was consistently ranging from 5 g/ml to 8.8g/ml with an average density of 8.2 g/ml, which is a good sign that the real density should be at that range near the average. As precise and consistent the results are, and how valid water displacement method is, there are some considerations that need to be noted while using this method. The density becomes more accurate the more times you measure the data. Small human errors and many other factors can affect the results. This means that the density must be measured multiple times while using the water displacement method. Also as stated before, many materials that react to water would not be suitable for this experiment, since these reactions can affect the accuracy of the data. With these considerations in mind, the data of our experiment shows that the water displacement method is a valid tool for measuring density
Conclusion
This paper examined the accuracy of the water displacement method to calculate the density of irregular shaped objects. The results showed that the water displacement method is a viable option for measuring density of an irregular shaped object, with the conditions that the object has low reactivity to water, and that the density is measured multiple times. A next test for future studies would be to analyze methods for objects of extreme sizes that cannot be measured visually, and a possible method for objects that have a high reactivity to water. A possible future experiment for items that react to water would be, to use another liquid instead that might not be as reactive. We can also retry the experiment with tools with more precision to get an even more accurate result.
Appendix
Aluminum Values
| # | Mass (grams) | Volume (milliliters) | Density (grams/milliliters) |
| 1 | 4.763 | 2 | 2.4 |
| 2 | 7.737 | 2.6 | 2.9 |
| 3 | 13.190 | 5 | 2.6 |
| 4 | 17.399 | 6 | 2.9 |
| 5 | 17.405 | 6.2 | 2.8 |
| 6 | 21.017 | 8 | 2.6 |
| Average Density | 2.7 |
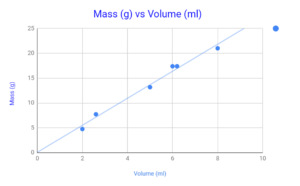
Figure 4 – Chart of Mass Vs Volume (Aluminum)
Unknown Sample Values
| # | Mass (grams) | Volume (milliliters) | Density (Grams/milliliters) |
| 1 | 42.512 | 5 | 8.5 |
| 2 | 47.845 | 5.5 | 8.7 |
| 3 | 53.185 | 6.8 | 7.8 |
| 4 | 55.788 | 7 | 7.9 |
| 5 | 69.049 | 8.6 | 8.0 |
| 6 | 71.750 | 8.8 | 8.2 |
| Average Density | 8.2 |
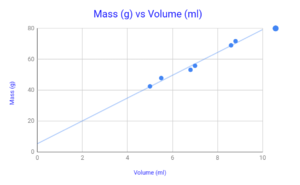
Figure 5 – Chart of Mass Vs Volume (Unknown Material)
List of Illustrations
Figure 1 Formula for Density, in terms of mass and volume——————– p. 4
Figure 2 Measuring Cylinder——————————————————– p. 5
Figure 3 Electronic Laboratory Balance——————————————- p. 6
Figure 4 Chart of Mass Vs Volume (Aluminum)——————————— p. 8
Figure 5 Chart of Mass Vs Volume (Unknown Material)———————– p. 8
Figure 6 Graph of Mass Vs Volume (Aluminum)——————————– p. 9
Figure 7 Graph of Mass Vs Volume (Unknown Material)———————- p. 9
References
Collection of free Formulas clipart density. Download on ubiSafe. (n.d.). Retrieved from
https://ubisafe.org/explore/formulas-clipart-density/
- Vinković, Roger W. Jones, Timmons Gotlieb, C.M. Allard, Robert B. Cody. (2006). Test
Method for Measuring density Volume of Apparent Density Cup Used in Test Methods B
212, B 329, and B 417
Electronic Laboratory Balance. (n.d.). Retrieved from
https://cdn.shopify.com/s/files/1/1357/0615/products/intell-lab-pm-300-precision-milligram-lab-balance_1024x1024.jpg?v=1472169780
Gupta, T., Yellishetty, M., & Singh, T. N. (2016). Measurement of Bulk volume and Density of
Irregular Solid Samples by Sand Displacement Method. Rock Mechanics and Rock
Engineering,50(3), 639-645. doi:10.1007/s00603-016-1104-z
- Moya-Larano, R. Macias-Ordonez, W.U. Blanckenhorn, C. Fernandez-Montraveta (2008).
Analysing body condition: mass, volume or density? Journal of Animal Ecology Vol 77.
Issue 6
Measuring Cylinder. (n.d.). Retrieved from
http://www.serrata.com.au/products/category/XLPLWHFG-measuring-cylinder
Shirin Mesbah Oskui, Heran C Bhakta, Graciel Diamante, Huinan Liu, Daniel Schlenk, &
William H Grover. (2017). Measuring the mass, volume, and density of microgram-sized
objects in fluid. PLoS ONE, 12(4), E0174068.


